Modelització senzilla d’una epidèmia (Mètode de Montecarlo)

Aquest petit article és senzillament un exercici, no pretén comparar-se amb les moltes modelitzacions en que epidemiòlegs i estadístics cerquen preveure els nous passos a fer en aquesta crisi que ens ha tocat viure. Aprofitant els dies de confinament, vaig pensar en fer un desenvolupament domèstic; però com cada dia la televisió està mostrant gràfiques, números i projeccions; vaig pensar en emular el que sortia per televisió.

Com sabem, la majoria de models es basen en plantejar un conjunt d’equacions diferencials, establir unes condicions d’entorn i fer-les evolucionar en el temps. D’epidemiologia no en sé, encara que últimament tots semblem experts; exceptuant el clàssic exercici d’equacions diferencials de l’epidèmia que puc trobar resolt a internet, poca cosa més podia aportar al meu model. Llavors vaig optar per un canvi d’estratègia, no usaria un model determinista si no un d’aleatori: el mètode Montecarlo. No invento res, de models estocàstics per epidèmies, webs, app... hi ha molts, només és un exercici.

Definició del model

En una àrea finita però no limitada (és a dir qui arriba al límit apareix per la paret contraria, així s’eliminen condicions de frontera) hi situem aleatòriament 10.000 caminants aleatoris. A cada iteració tots els caminants faran una passa aleatòria en direcció a algun dels vuit punts cardinals. Un (o alguns) d’aquests caminants tindrà l’estat “infectat”, el qual quan coincideixi amb un altre en estat “sa”, infectarà aquest amb probabilitat de contagi β=1. Cada nou “infectat” passarà a tenir el mateix comportament que el primer (cas origen). Aquest model és l’anomenat Susceptible Infecciós (SI). Definirem “dia” cada grup de 10 iteracions consecutives i serà el diferencial de temps.

Motor de successos (algoritme bàsic)

Caminant aleatori (2D)

És un objecte puntual situat en unes coordenades espaials al qual se’l desplaça de forma aleatòria en cada iteració. El desplaçament és produeix al sumar 1, 0 ó -1 al valor de les coordenades, el valor a escollir s'obté de forma random. La gràcia és que mentre alguns poden moure’s en distàncies compatibles al número d’iteracions la immensa majoria es desplacen dins d’un àrea no massa gran tal com es veu en les gràfiques següents. 

Òbviament el model de desplaçament pot ser tant complicat com sigui necessari, però pel meu model aquest comportament és similar al de les persones: algunes tenen alta mobilitat però la majoria sempre es mouen pels mateixos llocs. Tenint en compte les dimensions del marc on es mouen i les distància màxima recorreguda cap caminant acaba una volta complerta en les 1000 iteracions estàndard (eixos configuració més densa 200x150).

Model SI

Per fer la performance del model s’han disposat de quatre àrees que corresponen a les densitats de caminats: 0.1; 0.16; 0.20; 0.25 (per no carregar mostro les gràfiques del primer i l’últim). Al no tenir fronteres no té cap importància les dimensions reals.

Una cosa que s’observa és que quan menys densitat de caminants menys intensa és l’evolució de l’epidèmia, cosa que demostra que el distanciament és una bona manera de reduir la velocitat de contagis. En densitat 0.25 el pic de contagis és al dia 30 amb 521, mentre que 0.1 el té el dia 65 amb 135 (degut a la diferència d’escala els seus valors són els de la dreta).

Ser infectat no implica passar la malaltia. Els asimptomàtics no estan malalts encara que si són infecciosos. Per tant definim l’estat “malalt” (línia groga), estat que adquireix el 25% dels infectats aleatòriament quan s’infecten. De la mateixa manera poden estar hospitalitzats (línia verda) o no, i ho estan el 20% dels malalts. Els percentatges usats són els que estimaven del COVID-19 el dia que feia les simulacions, avui segurament seran diferents i tampoc és la meva idea emular aquesta epidèmia, simplement era agafar uns valors “raonables”. 

Malauradament el model SI és com “Walking Death” amb un macarró de gomaespuma com a única defensa, és a dir tothom acaba infectat. Però les epidèmies reals l’estat infectat/malalt no és per sempre, quan passa un temps evoluciona a un estat “curat” o malauradament “mort” (de moment els curo a tots). Defineixo pel model un “temps de malaltia” de 10 dies on un “infectat/malalt” passa a “curat”, estat que perd la condició d’infecciós però continua sent no-infectable. Amb aquestes condicions tornem a llençar el model amb els següents resultats.

Podem observar en aquest segon model anomenat Susceptible Infecciós Recuperat (SIR) la mateixa tendència que en el SI, la diferència està en que l’evolució presenta un màxim d’ infectats/malalts. Per simplificació de la gràfica continuo mostrant l’acumulat d’afectats (infecciosos) i la campana són només els malalts (recordo que els malalts només són el 25% dels infectats, per tant mai sobrepassa la línia d’infectats, en els casos que passa és perquè tenen escales diferents (malalts referenciats a l'escala de la dreta)).

El pic de malalts va dels 1.410 amb una punta d’infeccions diàries de 660 en densitat 0.33 fins als 703 malalts i 287 infeccions diàries per 0.16

Per aquest segon model he canviat la densitat de 0.1 per una més gran 0.33 degut a que la densitat 0.10 tendia a no esgotar el virus ni en 3000 iteracions. Quan s’esgota el virus? El criteri és malalts = curats, quan succeeix això no pot seguir la infecció per manca de RW contagiosos. En simulacions de baixes densitats s’arriba a esgotar el virus avanç d’assolir els 10.000 infectats, això és degut a que els últim infectats queden prou lluny dels pocs sans com per no atrapar-los avanç de recuperar-se, però solen quedar menys de 100 sans. El problema en el 0.1 era que avançava fins una densitat suficient de sans com per poder-se anar infectant en comptagotes.

El model corre, infecta, recupera i és pot mostrar en gràfiques però quan allunyat està d’un model real. Per això usarem un paràmetre anomenat Ritme Reproductiu (R0) i el compararem amb casos reals.

R0 (Ritme Reproductiu)

Obtenir aquest valor no ha estat senzill perquè hi ha diverses definicions quan s’aplica a un model epidèmic. Al final m’he decidit per la de  Hernández-Suárez: és el valor esperat de contactes sobre tot el temps d’activitat de la malaltia, entenent com contacte qualsevol interacció que pugui produir contagi. 

Així R0 la podem obtenir de l’expressió.

Aquest indicador mostra el ritme de creixement d’un període i un indicador d’evolució sent 1 el valor flat per sobre divergent (epidèmia imparable) i per sota convergeix a cero (s’extingirà). 

La probabilitat de contacte en el meu model és la densitat dividit pels passos (que són 10); la probabilitat de contagi és 1 i l’invers del temps d’infecció 10-1. R0 teòrica del model serà  la densitat x 10. 

Si ho apliquem a les densitats usades tindríem R0 de 1.6; 2.0; 2.5; 3.3; aquests són R0 compatibles amb malalties contagioses reals. Però aquest és un valor teòric, empíricament és aquesta R0 correcta. Per poder extreure la R0 de la definició hauria d’afegir més indicadors que complicarien el model, que no és l’objectiu. Per trobar-lo empíricament he anat a la definició general Nt=R0^t N0 

En la següent gràfica mostra l’evolució d’aquest paràmetre:

He avaluat períodes de cinc dies (t=5), tots decreixen excepte al principi degut a que comencem amb una xifra molt baixa (1 RW) i els primers cinc dies només es poden comparar amb l’infectat inicial.

 

El decreixement de la R0 el provoca l’efecte habitació. Si en una habitació tancada tenim 10 subjectes (9 sans 1 infectat) la projecció de la infecció seria 2n+n0: 1, 3, 7, 15? El màxim és 10; en realitat el que succeeix és que el primer té probabilitat 1 de contagi sobre els dos primers, però els dos nous infectats en realitat només tenen probabilitat 7/9 de poder infectar i els 3 següents (ja no seran quatre) serà només de 4/9. La sèrie més probable és 1, 3, 6, 9, 10.

Comportament del sistema sanitari

El model mostra un número de RW que necessiten hospitalització. La qüestió és Podran ser hospitalitzats? Agafant com exemple que a Catalunya hi ha 25 llits per cada 10.000 habitants agafo aquest valor assumint que hi haurà suficients sanitaris, medicines i serveis com per mantenir aquest valor constant.

Aplicant aquest valor al model s’obtenen els següents resultats per 0.20 i 0.25

En cada cas el sistema col·lapsa mancant 212 llits per 0.25 i 117 per 0.20 Col·lapsar significa que la gravetat del RW és tal que si no és atesa mor. Així doncs apliquem aquest estat.

Hospitalitzat no és un estat. A cada iteració s’avalua malalt per malat si estarà en hospital. Quan no queden llits el nou malalt que li toca hospital no serà atès i morirà, per no ser tant dur salvo un 10%.

En aquests dos casos l’epidèmia esdevé una catàstrofe: 2.045 morts en 0.2 (20% dels WR) i 2.143 morts pel 0.25.

Immunitat de grup

Afortunadament existeixen mecanismes de protecció natural que eviten un desastre com el descrit avanç. Un són les defenses naturals i una altre la immunitat provocada per haver passat la malaltia en fase tènue o les vacunes. La gràcia de la immunitat està en que tampoc cal que tothom la tingui. La immunitat de grup es produeix quan hi ha suficients individus immunes per evitar que arranqui l’epidèmia.

Per iniciar-se l’epidèmia cal una massa crítica per arrancar i per mantenir-se una altre. La primera necessita una densitat important de punt susceptibles perquè el primer RW infectat contamini els suficients per iniciar l’expansió avanç de curar-se. La segona simplement ha de ser lo suficientment gran com per poder trobar RW avanç de curar-se.

Les següents dues gràfiques mostren l’evolució per la densitat 0.20 amb inmunitat del 75% i 90% de la població. Per evitar la fallida de l’arrancada comencen amb 5 RW infectats

Per sota del 75% comencen haver col·lapses del sistema sanitari. La gràfica del 75% de confinament encara mostra una epidèmia, que no col·lapsa, però que és capaç d’infectar 2.109 (84% dels susceptibles no immunitzats) i un pic de 81 malalts. No és fins al voltant del 90% que els cinc infectats es queden sense recorregut; en el cas que mostro 28 són els infectats i el pic de malats és 3.

Confinament

Si no tenim població immunitzada ho hem de fer de forma artificial. Per fer-ho cal posar barreres de protecció, en aquest cas hauria de fer una β variable i per grups. Una altre és baixar la massa crítica del sistema com feien els RW immunes. En comptes de fer una β variable he optat per crear un estat “confinat” el qual inhibeix tota interacció amb la resta de RW, al acabar aquest estat actualitza els cronometres i retorna al estat que li pertocaria. 

El procés de confinament és independent de l’estat, el RW que se li assigna ser confinat perd el seu estat i passa a confinat, quan s’aixeca el confinament se li retorna l’estat que tenia excepte si el seu estat original era evolutiu (exemple infectat/malalt) llavors li afegirà al cronòmetre el temps de confinament se i li aplicarà el canvi que pertoqui.

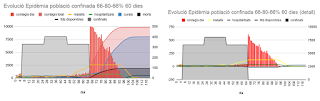
Sobre la densitat de 0.20 es fan quatre performances (no mostro els infectats i curats):

Es pot observar que influeix més el percentatge de confinats que no el temps de confinament. Ambdós condicionants no són capaços d’evitar un rebrot i posterior col·lapse si no són lo suficientment potents per extingir l’epidèmia durant el període, quelcom que en l’anterior apartat veiem que es produïa només amb el 90% d’immunitat.

Curiosament el rebrot més important és en 66% 40 dies. El motiu és doble, primer el 66% de confinament no atura el creixement per tant hi ha molts infectats quan s’alliberen els confinats; el segon és la mobilitat quant més temps passa més ben distribuïts en l’espai estan els infectats, quan s’alliberen aquests infectats troben “habitacions” més densament poblades de susceptibles que quan s'expandeix lliurament que ocupen tots els infectats una part de l’espai

L’evolució del paràmetre R0 mostra com en confinaments de 20 dies la major part de temps te R0 superior a 1 

Aquesta vall al inici dels confinaments la provoca la desaparició sobtada dels infectats/malalts que són confinats. En el món real això no passa perquè compten només els malats però no els  asimptomàtics. En la realitat tots els malats estan confinats, encara que parcialment perquè contagien familiars i sanitaris; això és difícil de parametritzar (el meu model és simple), per tant infectats i malalts són iguals a efectes d’infecció en el meu model, cosa que distorsiona la R0 al inici del confinament, a partir del màxim local (dia 11) l’evolució és correcta.

En aquest vídeo es pot veure una evolució complerta amb un confinament del 80% durant 30 dies començant 10 dies desprès de declarada l'epidèmia.

Un cas de multi període confinament

Com a exemple mostro la evolució amb tres períodes de confinament, (66%-80%-66%) de 20 dies cada un, per la densitat de 0.20

Es pot observar que en 80% de confinament el número d'infectats es manté però al 66% aquests comencen a augmentar dia a dia fins l'esclat al acabar el confinament.

Conclusió

Aquest model d’epidèmia té una evolució ràpida en el temps, que produeix un col·lapse del sistema sanitari; produint una mortaldat al voltant del 20%, no per la letalitat de la malaltia, si no pel col·lapse en sí. 

A manca de defensa natural immunitària, la qual comença a ser efectiva a partir del 75% de població immunitzada, s’imposa la necessitat de mesures de barrera, el confinament o les quarantenes. 

Pels confinaments generals és necessari un període posterior de immunització controlada, perquè alliberar de cop la població fa que l’epidèmia reprengui. Una segona possibilitat és fer un confinament el suficientment llarga com per exhaurir la infecció; tanmateix s’ha de comptar amb un fet que quan més baixa és la densitat més li costa exhaurir-se l’epidèmia (mirar primeres gràfiques).

Per acabar dir, que és un model matemàtic que assumeix certes premisses raonables, però no necessàriament reals. No és cap pronòstic del que pot passar. Només mostro una altre manera de modelitzar, sense resoldre les equacions diferencials o desconeixent-les.

Nota: Hernández‐Suárez CM. A Markov chain approach to calculate R0 in stochastic epidemic models. J Theor Biol 2001;215:83‐93